La méthode des clés aléatoires
Une alternative aux méthodes suppressives ?
DMS/DMRG
03/10/2024
1 Les enjeux
Les méthodes suppressives
Les enjeux
Exemple d’application de la méthode suppressive
| Catégorie \ Sexe | Hommes | Femmes | Total |
|---|---|---|---|
| ABC | 1 | 10 | 11 |
| DE | 12 | 14 | 26 |
| Total | 13 | 24 | 37 |
| Catégorie \ Sexe | Hommes | Femmes | Total |
|---|---|---|---|
| ABC | s | s | 11 |
| DE | s | s | 26 |
| Total | 13 | 24 | 37 |
Les outils utilisés: $\tau$-Argus (CBS) et rtauargus (développé à la DMRG)
Limites des méthodes suppressives
Les enjeux
Pour l’utilisateur :
- Est privé d’une partie de l’information, parfois non négligeable;
- Ne peut pas manipuler lui-même les données;
- Est frustré par les restrictions éventuelles de la diffusion (finesse, zonages, etc.)
Limites des méthodes suppressives
Les enjeux
La différenciation géographique
- Nécessite des traitements complémentaires
- Traitements lourds et fastidieux
- Vraie limite quand il faut diffuser plusieurs zonages à la fois
- Principal enjeu de l’expérimentation sur les QPV
- \(\rightarrow\) cf Présentation séminaire DMS du 10 février 2023
Limites des méthodes suppressives
Les enjeux
Le problème de la diffusion sur mesure
- Théoriquement:
- Prendre en compte le secret posé dans les tableaux déjà diffusés (en diffusion standard ou en diffusion sur mesure);
- \(\Rightarrow\) la quantité de secret augmente mécaniquement
- Dans la pratique:
- On traite les demandes indépendamment les unes des autres
- \(\Rightarrow\) risques de divulgation non maîtrisés
Limites des méthodes suppressives
Les enjeux
Autres limites
- La complexité des traitements augmente avec la complexité de la diffusion:
- Nombre de tableaux
- Liens entre variables (marges, équations)
- Hiérarchies / Hiérarchies non emboîtées
- \(rightarrow\) cf l’exemple de l’enquête TIC présenté à la conférence NTTS 2023
- Une charge de la pose du secret qui repose sur l’aval de la chaîne.
- Des outils (en particulier \(\tau\)-Argus) qui touchent à leurs limites.
Nos besoins
Les enjeux
➡️ Pour répondre au mieux aux enjeux actuels et futurs, on recherche une méthode qui :
- Offre un niveau de protection similaire;
- Réduit par elle-même le risque de différenciation géographique;
- Protège adéquatement la diffusion sur mesure;
- Centralise les traitements de la confidentialité;
- Est relativement simple à implémenter et à généraliser pour des cas d’usage divers.
Quelles alternatives sont à notre disposition ?
Les enjeux
Aller chercher ailleurs
Aucune méthode suppressive ne répondra aux enjeux 2 à 5 sauf à réduire drastiquement la diffusion.
\(\Rightarrow\) Chercher une solution du côté des méthodes perturbatrices
Quelles alternatives sont à notre disposition ?
Les enjeux
| diff géo | sur mesure | central. | implément. | |
|---|---|---|---|---|
| Arrondi des petits comptages | Non | Non | Non | Oui |
| Target Record Swapping | Non | Oui | Oui | Non |
| Arrondi déterministe | Oui | Oui | Oui | Oui |
| Arrondi aléatoire | Oui | Non* | Oui | Oui |
| Mécanisme de bruit DP | Oui | Oui* | Oui | Non* |
| Données synthétiques | Oui | Oui | Oui | Non |
| Méthodes des clés aléatoires | Oui | Oui | Oui | Oui |
Mais il y a un prix à payer
Les enjeux
Incohérence des requêtes entre elles
Pour certaine méthode, deux requêtes successives peuvent fournir des informations différentes.
Mais il y a un prix à payer
Les enjeux
Inconsistance des comptages entre eux
Par exemple, Si \(H+F=T\), toutes les méthodes ne garantissent pas que \(H' \leq T'\) et que \(F' \leq T'\).
(\(H'\) étant la version perturbée de \(H\)).
Mais il y a un prix à payer
Les enjeux
Perte d’additivité
Si \(H+F=T\), toutes les méthodes ne garantissent pas que \(H'+F'=T'\).
Mais il y a un prix à payer
Les enjeux
Inconsistance des ratios (découle des deux points précédents):
Par exemple, \(\frac{H'}{T'} > 1\) ou \(\frac{H'}{T'} > 1\)
Mais il y a un prix à payer
Les enjeux
| requêtes | comptages | additivité | |
|---|---|---|---|
| Arrondi des petits comptages | Non | Oui* | Oui* |
| Target Record Swapping | Oui | Oui | Oui |
| Arrondi déterministe | Oui | Oui | Oui |
| Arrondi aléatoire | Non | Non | Non |
| Mécanisme de bruit DP | Non | Oui* | Non |
| Données synthétiques | Oui | Oui | Oui |
| Méthodes des clés aléatoires | Oui | Non | Non |
Le compromis Risque-Utilité
Les enjeux
Cadre de l’intervention
Principes de la méthode
- Données tabulées, c’est-à-dire agrégées
- Données de comptage, c’est-à-dire sans pondération ni volumes
2 Les principes de la méthode des clés aléatoires
Pourquoi utiliser cette méthode ?
👍 Avantages de la méthode des clés aléatoires
- Méthode perturbatrice systématique:
- \(\Rightarrow\) Réduction automatique du risque de différenciation
- Paramétrage par le producteur du bruit injecté
- \(\Rightarrow\) Arbitrage objectif du compromis Risque/Utilité
- Utilisation de clés individuelles
- \(\Rightarrow\) Cohérence des requêtes
- \(\Rightarrow\) Consistance d’une diffusion sur mesure avec une diffusion standard
- Facilité d’implémentation
- \(\Rightarrow\) Réduction de la charge des traitements liés à la confidentialité
- Centralisation des traitements
- \(\Rightarrow\) Traitements réalisés en amont et non en aval
- \(\Rightarrow\) Charge “mentale” de la confidentialité ne repose plus sur les chargés de la diffusion mais sur le producteur.
Pourquoi ne pas utiliser cette méthode ?
👎 Limites de la méthode des clés aléatoires
- Méthode perturbatrice systématique:
- \(\Rightarrow\) Toutes les cases de tous les tableaux sont perturbées (perte d’utilité)
- Bruitage indépendant des cases:
- \(\Rightarrow\) Perte d’addivité
- \(\Rightarrow\) Inconsistance possible des comptages entre eux
- \(\Rightarrow\) Inconsistance possible des ratios ou des évolutions.
Remarque
La Perte d’addivité peut aussi être vue comme une mesure supplémentaire de protection
Origine et Usages de la méthode
- Méthode développée par l’Australian Bureau of Statistics (ABS) en 2005 ([2], [6])
- Développements complémentaires par Destatis ([4], [5], [7])
- packages R:
ptableetcellKey - travaux pour adapter la méthode sur des variables quantitatives
- packages R:
- Usages:
- TableBuilder d’ABS
- Outil de requêtage en ligne des données du recensement depuis 2006
- D’autres bases de données disponibles
- Census Européen 2021:
- Méthode utilisée par plusieurs INS européens
- dont Destatis pour les données carroyées (sans restauration d’additivité)
- TableBuilder d’ABS
Quelques notations
Principes de la méthode
- \(X \in \mathbb{N}=\{0;1; \dots \}\) un comptage original
- \(X'\in \mathbb{N}\) le comptage perturbé de \(X\)
- \(p_{ij} = \mathcal{P}(X ' = j | X = i)\) la probabilité de transition de \(i \rightarrow j\)
Probabilité de transition
\(p_{ij}\) est la probabilité que le comptage après perturbation soit \(j\) si le compte original vaut \(i\).
Quelques notations
Principes de la méthode
- \(D\) la déviation maximale autorisée de \(i\)
- \(\Rightarrow |j-i| \leq D\)
- \(V\) la variance fixe du bruit qu’on souhaite injecter
Paramètres de la méthode
- \(D\) et \(V\) sont deux paramètres fixés par l’utilisateur.
- Ils permettent de gérer le compromis Risque-Utilité.
Comment est tiré \(j\) ?
Principes de la méthode
- Pour obtenir la valeur de \(X'|X=i\),
- On doit définir une distribution de probabilités \(\mathcal{P}(X '| X = i)\)
- On tire aléatoirement une valeur \(j\) selon cette distribution.
- La perturbation est injectée dans chaque cellule d’un tableau de manière indépendante.
Effet d’une déviation injectée indépendamment dans chaque cellule
| Catégorie \ Sexe | Hommes | Femmes | Total |
|---|---|---|---|
| ABC | 1 | 10 | 11 |
| DE | 12 | 14 | 26 |
| Total | 13 | 24 | 37 |
| Catégorie \ Sexe | Hommes | Femmes | Total |
|---|---|---|---|
| ABC | 0 | 11 | 13 |
| DE | 14 | 13 | 26 |
| Total | 12 | 22 | 35 |
Construction de la loi de probabilités (Cas général)
Principes de la méthode
\(D\) et \(V\) étant fixés, pour une valeur originale \(i \geq D\) (cas général),
On cherche à déterminer les \(p_{ij} = \mathbb{P}(X'=j|x=i)\) avec:
- une loi de probabilité d’entropie maximale
- un univers de la distribution \(j \in \{i-D; \dots; i+D\}\)
- une distribution sans biais
- une distribution de variance \(V\)
Construction de la loi de probabilités
Principes de la méthode
\(D\) et \(V\) étant fixés, pour une valeur originale \(i\), on cherche la distribution de probabilités des \(p_{ij}\) tels que:
\[\begin{equation} \begin{aligned} \max_{p_{ij}} \quad & \sum_{j=i-D}^{i+D}{p_{ij} \cdot \log(p_{ij})}\\ \textrm{s.t.} \quad & \sum_{j=i-D}^{i+D}{ p_{ij}} = 1\\ & \mathbb{E}[X'|X=i] = \sum_{j=i-D}^{i+D}{ j \cdot p_{ij}} = i\\ & \mathbb{V}[X'|X=i] = V \\ \end{aligned} \end{equation}\]
Construction de la loi de probabilités
Principes de la méthode
Remarques
- Il s’agit du programme d’optimisation implémenté dans le package
ptable. - Dans les faits, il n’existe pas une solution sans biais pour chaque couple \((D,V)\) fixé.
- On utilise la même distribution pour tous les \(i \geq D\).
Exemples de distribution de probabilités
Principes de la méthode
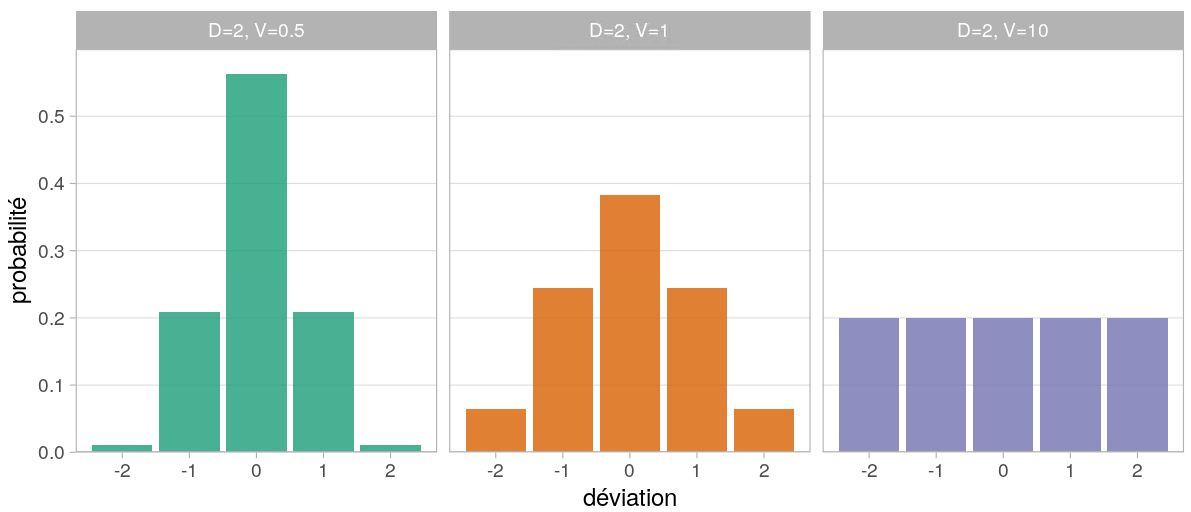
Figure 1: Distributions de probabilités pour \(D=2\) et trois valeurs de \(V\) (cas général où \(X = i \geq 2\))
Le rôle de la variance
Principes de la méthode
| Scénario 1 (Vert) | Scénario 2 (Orange) | Scénario 3 (Violet) | |
|---|---|---|---|
| Variance | 0.5 | 1 | 10 |
| % de chances qu’une valeur ne soit pas déviée | 56% | 38% | 20% |
| % de chances qu’une valeur subisse une déviation maximale (-2 ou +2) | 2% | 13% | 40% |
| Conservation de l’information | ++ | + | – |
| Niveau de protection | – | + | ++ |
Remarque
\(D\) et surtout \(V\) ont une influence directe sur le compromis Risque/Utilité.
Construction de la loi de probabilités
Principes de la méthode
Dans le cas où \(i < D\),
- la plage des valeurs possibles de \(X'|X=i\) est \(\{0; \dots; i+D\}\).
- le nombre de valeurs à disposition dépend de \(i\)
- Si \(D=3\), alors \(X'|X=1\) prendra ses valeurs dans \(\{0;1;2;3;4\} \Rightarrow 5\) valeurs possibles.
- Si \(D=3\), alors \(X'|X=2\) prendra ses valeurs dans \(\{0;1;2;3;4;5\} \Rightarrow 6\) valeurs possibles.
- Cas général: Si \(D=3\), alors \(X'|X=i, i\geq 3\) prendra ses valeurs dans \(\{i-3;i-2;i-1;i;i+1;i+2;i+3\} \Rightarrow 7\) valeurs possibles.
- Si \(D=3\), alors \(X'|X=1\) prendra ses valeurs dans \(\{0;1;2;3;4\} \Rightarrow 5\) valeurs possibles.
- la contrainte sur la variance \(V\) devient \(\mathbb{V}[X'|X=i] \leq V\).
- \(\Rightarrow\) Nécessité de définir \(D\) distributions de probabilités.
Un exemple de matrice de transition
Principes de la méthode
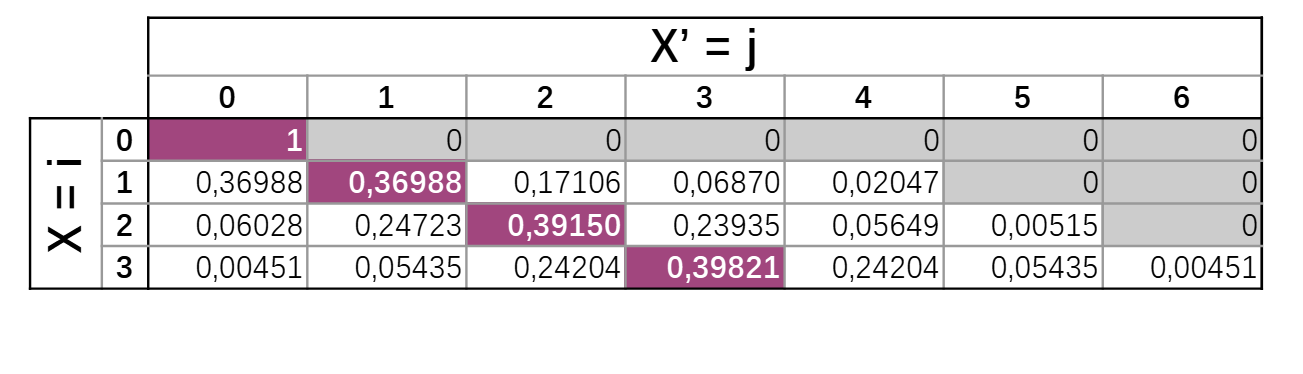
Matrice de transition pour \(D=3\) et \(V=1\)
Un exemple de matrice de transition
Principes de la méthode
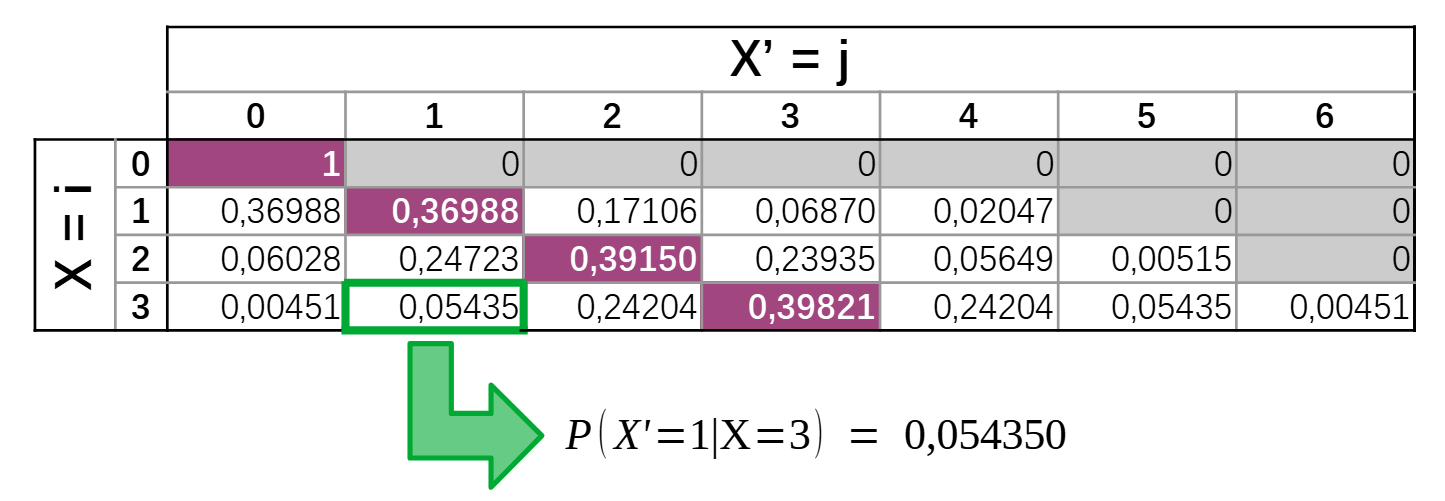
Matrice de transition pour \(D=3\) et \(V=1\)
Caractéristiques
Principes de la méthode
- Bruit sans biais et de variance fixée par l’utilisateur
- Toutes les cellules sont perturbées
- Les comptages perturbés sont \(\geq 0\)
- Un comptage non nul peut devenir nul après perturbation
- Un comptage original nul n’est pas perturbé
Les clés aléatoires
Principes de la méthode
Le mécanisme de bruitage ne suffit pas !
Deux requêtes identiques réalisées successivement ne fourniront pas le même résultat.
\(\Rightarrow\) Il n’assure de lui-même pas la cohérence des requêtes entre elles.
Les clés aléatoires
Principes de la méthode
Le mécanisme de bruitage ne suffit pas !
Deux requêtes identiques réalisées successivement ne fourniront pas le même résultat.
\(\Rightarrow\) Il n’assure de lui-même pas la cohérence des requêtes entre elles.
Solution proposée par la CKM
- Ajouter des clés aléatoires aux individus:
- par tirage iid uniforme dans \([0;1]\)
- Faire dépendre la perturbation d’une cellule de la valeur des clés des individus qui la composent
Le processus complet de bruitage
Principes de la méthode
Le processus de bruitage de la méthode des clés aléatoires peut être décomposé en \(4\) étapes:
- Tirer les clés aléatoires individuelles
- Construire le tableau en dénombrant les individus et en agrégeant les clés
- Construire une table de perturbation à partir de la matrice de transition
- Déduire la perturbation à appliquer en fonction des étapes 2 et 3
Etape 1: Tirer les clés aléaores individuelles
Le processus complet de bruitage
| id | Commune de résidence | Âge | Clé |
|---|---|---|---|
| 1 | Amiens | 25 | 0,9177275 |
| 2 | Paris | 20 | 0,8850062 |
| 3 | Marseille | 45 | 0,6266963 |
| 4 | Amiens | 45 | 0,1117820 |
| 5 | Marseille | 20 | 0,6496634 |
| 6 | Marseille | 20 | 0,2813433 |
Etape 2: Construire le tableau
Le processus complet de bruitage
On dénombre les individus et on agrège les clés.
| Commune de résidence | ids | Effectif | Somme des clés | Clé de la case |
|---|---|---|---|---|
| Amiens | {1,4} | 2 | 1,0295095 | 0,0295095 |
| Marseille | {3,5,6} | 3 | 1,5577030 | 0,5577030 |
| Paris | {2} | 1 | 0,8850062 | 0,8850062 |
| Total | {1,2,3,4,5,6} | 6 | 2,7722187 | 0,7722187 |
Etape 2: Construire le tableau
Le processus complet de bruitage
Clé de cellule - Cell Key
Une clé est associée à chaque cellule d’un tableau:
- Si \(rk_k\) est la clé de l’individu \(k\) et \(ck_c\) la clé de la cellule \(\mathbf{C}\), alors
- La somme des clés individuelles de la cellule s’écrit: \(Sk_c = \sum_{k \in \mathbf{C}} rk_k\)
- La clé de la cellule vaut: \(ck_c = Sk_c - \left \lfloor{Sk_c}\right \rfloor\)
- On peut montrer que si les \(rk_k \sim \mathcal{U}(0,1)\) iid alors \(ck_c \sim \mathcal{U}(0,1)\)
Etape 3: Construire une table de perturbation
Le processus complet de bruitage
A partir de la matrice de transition obtenue pour \(D=2\) et \(V=1\):
| Effectif original | dev.=-2 | dev.=-1 | dev.=0 | dev.=+1 | dev.=+2 |
|---|---|---|---|---|---|
| 1 | 0,37 | 0,36 | 0,17 | 0,1 | |
| 2 ou plus | 0,06 | 0,25 | 0,38 | 0,25 | 0,06 |
Etape 3: Construire une table de perturbation
Le processus complet de bruitage
On en déduit la table de perturbation suivante:
| Effectif original | dev.=-2 | dev.=-1 | dev.=0 | dev.=+1 | dev.=+2 |
|---|---|---|---|---|---|
| 1 | [0 ; 0,37[ | [0,37 ; 0,73[ | [0,73 ; 0,9[ | [0,9 ; 1[ | |
| 2 ou plus | [0 ; 0,06[ | [0,06 ; 0,31[ | [0,31 ; 0,69[ | [0,69 ; 0,94[ | [0,94 ; 1[ |
Exemple
\(X = 2\) et \(ck_c = 0,25 \in [0,06 ; 0,31]\), alors \(X' = 2 - 1 = 1\)
Etape 4
Le processus complet de bruitage
Pour chaque cellule, on repère la déviation à appliquer dans la table de perturbation en fonction de \(i\) et de la clé.
| Clé de la case | Intervalle de Perturbation | Effectif | Bruit à injecter | Effectif perturbé | |
|---|---|---|---|---|---|
| Amiens | 0,0295095 | [0 ; 0,06[ | 2 | -2 | 0 |
| Marseille | 0,5577030 | [0,31 ; 0,69[ | 3 | 0 | 3 |
| Paris | 0,8850062 | [0,73 ; 0,9[ | 1 | +1 | 2 |
| Total | 0,7722187 | [0,69 ; 0,94[ | 6 | +1 | 7 |
Extra
Le processus complet de bruitage
En calculant les effectifs par âge et en leur appliquant le processus décrit plus haut, on obtient la perturbation présentée dans le tableau 9, dans lequel on observera que le total est perturbé exactement de la même manière que dans le tableau 8.
| Âge | ids | Clé de la case | Effectif | Bruit à injecter | Effectif perturbé |
|---|---|---|---|---|---|
| 20 | {2,5,6} | 0,8160129 | 3 | +1 | 4 |
| 25 | {1} | 0,9177275 | 1 | +2 | 3 |
| 45 | {3,4} | 0,7384783 | 2 | +1 | 3 |
| Total | {1,2,3,4,5,6} | 0,7722187 | 6 | +1 | 7 |
Le compromis Risque-Utilité
Principes de la méthode
Comment mesurer l’utilité ?
- Distance entre le tableau original et le tableau perturbé (distributions empiriques des comptages):
- distance de Hellinger
- distance de Bhattacharyya
- On peut aussi tester la robustesse d’analyses statistiques avant/après:
- Stabilité du \(V\) de Cramer
- Superposition du nuage des modalités sur le premier plan factoriel d’une AFC
- \(\rightarrow\) cf Rapport de stage de Thomas Gardair
Bref, il existe de nombreuses façons de le faire.
Le compromis Risque-Utilité
Principes de la méthode
Comment mesurer le risque ?
- Risque principal est porté sur les petites cellules
- Car facilite une éventuelle réidentification
- Sens des règles fixant un seuil de confidentialité
Les probabilités de transition inverses
La probabilité \(q_{ij} = \mathcal{P}(X = i | X' = j)\) mesure la capacité d’un attaquant à deviner la vraie valeur de la cellule (\(X=i\)) étant donnée la valeur qui est diffusée (\(X'=j\)).
Par la formule de Bayes, on peut exprimer les \(q_{ij}\) en fonction des \(p_{ij}\):
\[q_{ij} = \mathcal{P}(X=i | X'=j) = \frac{\mathcal{P}(X'=j | X=i) \mathcal{P}(X=i)}{\mathcal{P}(X'=j)} = \frac{p_{ij} \mathcal{P}(X=i)}{\sum_k{p_{kj}\mathcal{P}(X=k)}}\]
3 Résultats issus de l’expérimentation sur les QPV
Contexte de l’expérimentation
Expérimentation QPV
- Diffusion des données sur les QPV contours 2015 et 2024
- Sur toutes les sources sauf Filosofi et le RP
- Un travail conjoint avec la DSAU
- Comparaison de méthode des clés aléatoires avec des méthodes d’arrondis
- Validation en CD du choix de la CKM pour la diffusion fin 2024.
Motivation principale du chanegement de méthodes
Diffusion des QPV sur deux millésimes de contours:
- de nombreux QP 2024 ont des contours proches des QP 2015 \(\Rightarrow\) nombreux problèmes de différenciation géographique
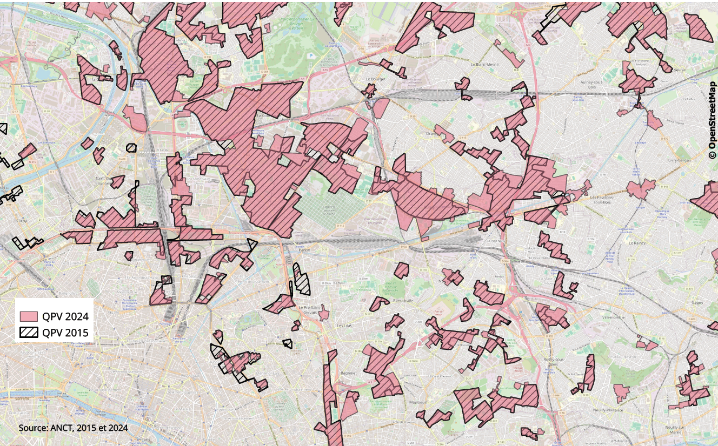
Figure 2: Superposition des deux zonages en Île-de-France
Comparaison aux arrondis
Expérimentation QPV
Jeu de données : Pôle Emploi
Seuil de confidentialité : 5
Expérimentation réalisée sur \(6\) tableaux composés de \(\sim 395 000\) cellules uniques non nulles.
Méthodes envisagées:
- Arrondi déterministe
- Arrondi aléatoire
- Clés aléatoires
Mécanismes probabilistes
Le mécanisme de perturbation de ces méthodes peut être décrit par des probabilités de transition \(p_{ij}\)
L’arrondi déterministe
Expérimentation QPV

Extrait d’une matrice de transition pour arrondi déterministe de base \(5\)
L’arrondi aléatoire
Expérimentation QPV

Extrait d’une matrice de transition pour arrondi aléatoire de base \(5\)
Ensemble de déviation vs Ensemble des possibles
Expérimentation QPV
Définition
L’ensemble de déviation d’une valeur \(i\), noté \(\mathcal{D}_i\), est l’intervalle des valeurs qu’elle peut prendre après application de la perturbation.
Exemple: Si on arrondit aléatoirement \(i=8\) dans une base \(10\), l’ensemble de déviation \(\mathcal{D}_8 = \{ 0; 10\}\)
Définition
L’ensemble des possibles d’une valeur perturbée \(j\), noté \(\mathcal{D'}_j\), est l’intervalle des valeurs originales dont elle est possiblement issue.
Exemple: Si après l’application d’un arrondi aléatoire de base \(10\), \(j=0\), alors l’ensemble des possibles est \(\mathcal{D'}_0 = \{ 0; 1; 2; \dots 9 \}\).
\(\Rightarrow\) Permettent une première comparaison des trois méthodes.
Les scénarios comparés
Expérimentation QPV
L’expérimentation a consisté à comparé plusieurs scénarios:
- un arrondi déterministe (\(Base = 20\))
- un arrondi aléatoire (\(Base = 10\))
- une CKM classique (\(D = 10\) et \(V = 6.25\))
- une CKM où certaines valeurs sont interdites (\(D = 10\), \(V = 6.25\))
- une combinaison CKM (\(D=5\)) + arrondi déterministe (\(Base = 5\))
Motivations du choix des paramètres
Expérimentation QPV
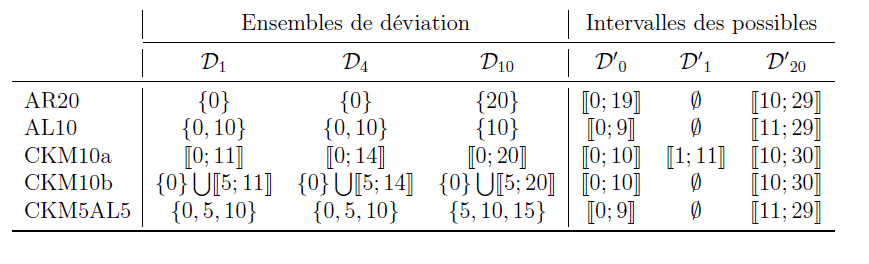
Figure 3: Comparaison des ensembles de déviation et des possibles des trois méthodes
Comportements des scénarios
Expérimentation QPV
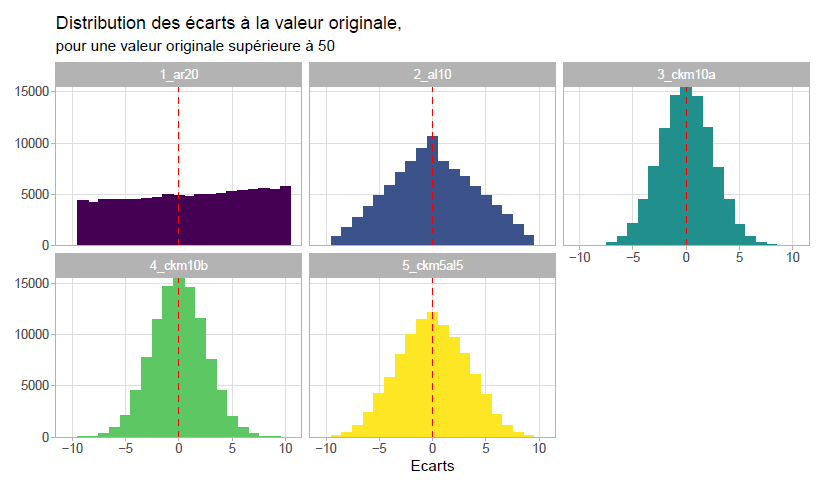
Figure 4: Distributions des déviations observées
Compromis Biais/Variance
Expérimentation QPV
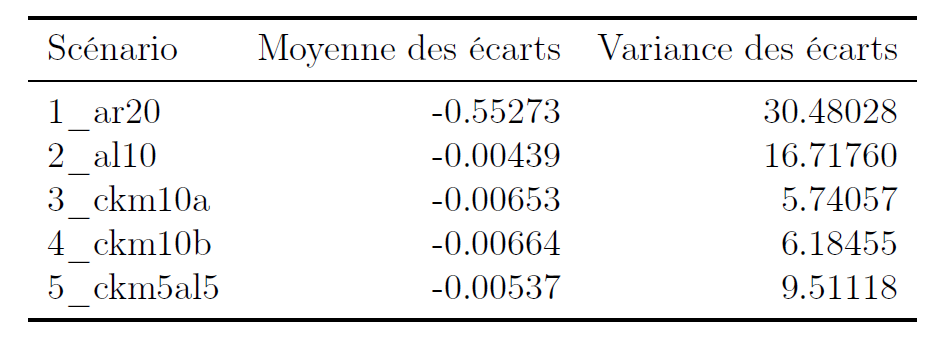
Figure 5: Les méthodes d’arrondi ont une variance empirique très supérieure aux CKM
Utilité 1: Distance entre original et perturbé
Expérimentation QPV
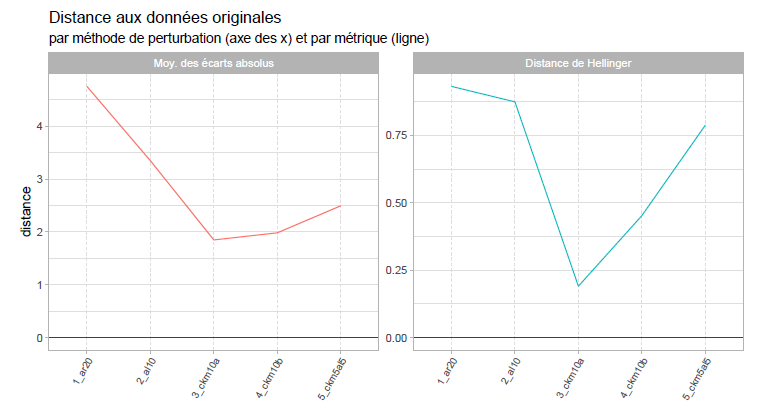
Figure 6: Les méthodes basées sur la CKM offrent une meilleure utilité sur le critère des distances entre tableaux
Utilité 2: L’additivité de façade sur la variable SEXE
Expérimentation QPV
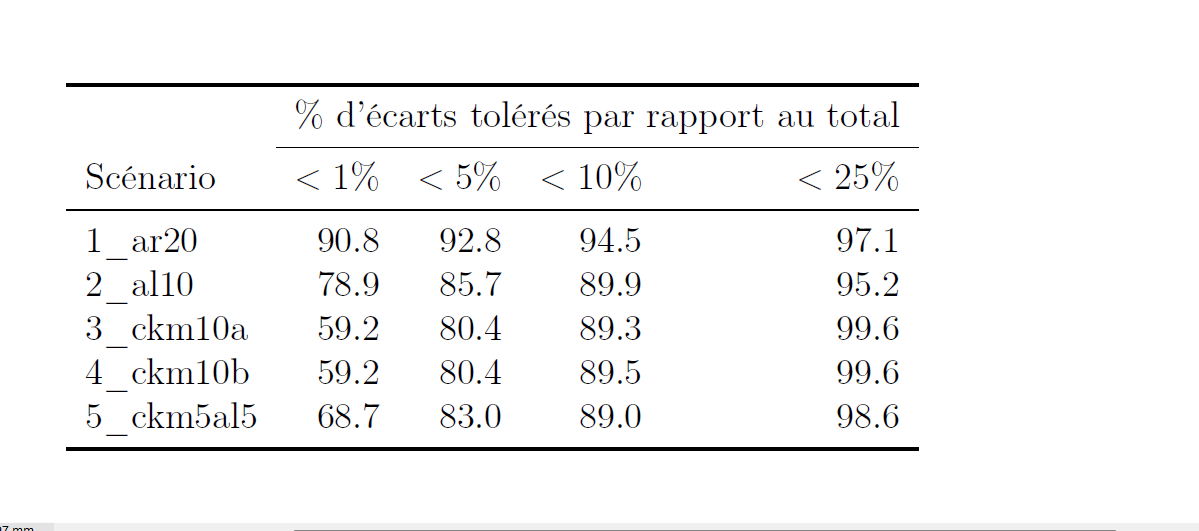
Figure 7: Pour une variable à 2 modalités, les arrondis génèrent moins d’écarts à l’additivité
Utilité 3: L’additivité de façade sur la variable CATEG
Expérimentation QPV
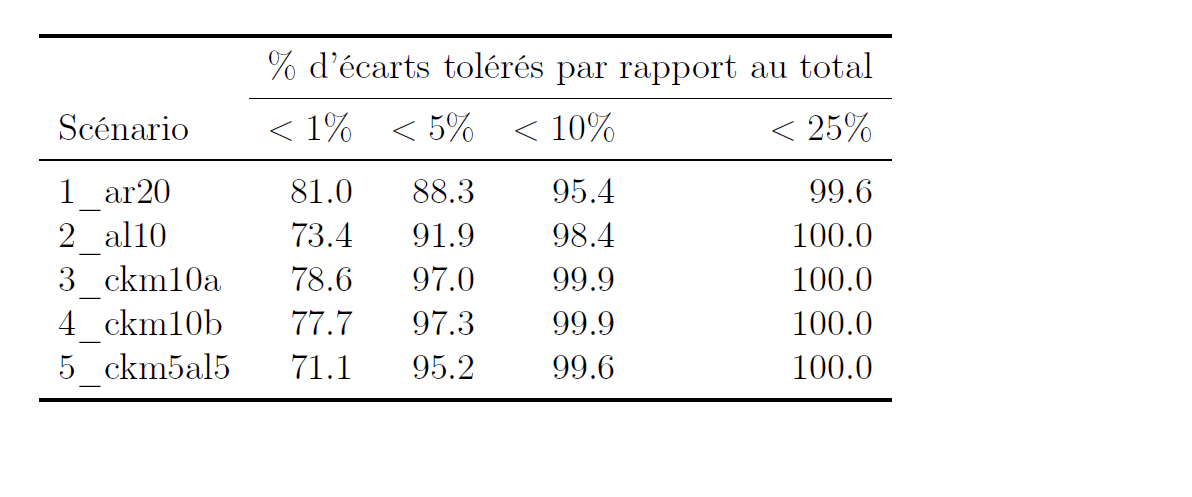
Figure 8: Pour une variable à 5 modalités, les CKM génèrent moins d’écarts à l’additivité
Risque: La capacité d’inférence sur les valeurs sensibles
Expérimentation QPV
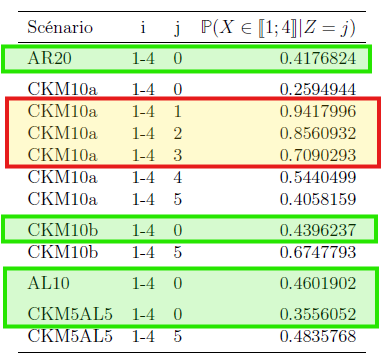
Figure 9: Pour une CKM classique, le risque d’inférence des valeurs sensibles est très élevé. Il est mieux contrôlé par les autres mécanismes.
Bilan
Expérimentation QPV
- Arrondi déterministe:
- Choix d’une base élevée pour un niveau de protection similaire
- Pas de paramétrage de la variance
- Méthode la moins performante en temres d’utilité
- Arrondi aléatoire:
- Choix d’une base similaire au \(D\) de la CKM
- Pas de paramétrage de la variance
- Utilité: une perte d’information plus importante que les CKM
- Additivité: meilleure pour des variables à peu de modalités
- Difficulté d’implémentation pour assurer une diffusion à la demande (Comment assurer qu’une même requête donne toujours le même résultat ?)
Bilan
Expérimentation QPV
- CKM classique:
- Le meilleur scénario en termes d’utilité
- Le niveau de risque d’inférence des valeurs sensibles est trop élevé
- CKM avec valeurs sensibles (1-4) interdites:
- Le 2nd meilleur scénario en termes d’utilité (et 1er ex aequo pour \(i>20\))
- Niveau de risque d’inférence des valeurs sensibles équivalent à l’arrondi aléatoire.
- CKM + arrondi:
- Pas convaincant en termes d’utilité
- Niveau de risque d’inférence des valeurs sensibles équivalent à l’arrondi aléatoire.
Bilan du bilan
Expérimentation QPV
Choix de la CKM avec valeurs sensibles interdites
- Tous les avantages de la méthode des clés aléatoires
- Une très bonne conservation de l’information
- Un niveau de protection contre la divulagtion par inférence identique aux méthodes d’arrondis
Pour finir de se convaincre
Expérimentation QPV
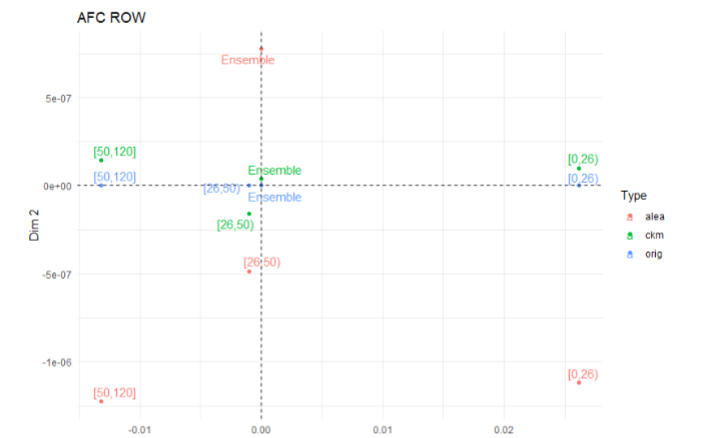
Figure 10: Projection des modalités de la variable d’âge sur le premier plan factoriel d’une AFC
4 Les perspectives
En termes d’usage
Perspectives
Concrètement :
- Diffusion sur mesure : expérimentation sur la BTS d’ici septembre 2025
A terme ?
- Une méthode parfaitement adaptée aux requêtages multiples
- avec quelques précautions du type nombre de croisements.
- Implémentation dans Aïda ?
- Systématisation pour la réponse à la demande ?
- Proposition auprès des PSAR quand ils mettent à disposition des données auprès des SED ? …
En termes de travaux
Expérimentation QPV
- Un package adapté pour les usages en interne (en cours de développement)
- Généraliser le choix des paramètres en fonction des règles de confidentialité
- Données pondérées (Recensement, enquête)
- Expérimentations sur variables quantitatives (volumes) à partir des travaux de Destatis
- Indicateurs (moyennes, quantiles, etc.)
Références bibliographiques
Références (1)
Références bibliographiques
[1] F. Bach, “Differential Privacy and Noisy Confidentiality Concepts for European Population Statistics”, Journal of Survey Statistics and Methodology, vol. 10, nᵒ 3, p. 642‑687, juin 2022, doi: 10.1093/jssam/smab044.
[2] J. Chipperfield, D. Gow, et B. Loong, “The Australian Bureau of Statistics and releasing frequency tables via a remote server”, SJI, vol. 32, nᵒ 1, p. 53‑64, févr. 2016, doi: 10.3233/SJI-160969.
[3] V. Costemalle, “Detecting geographical differencing problems in the context of spatial data dissemination”, SJI, vol. 35, nᵒ 4, p. 559‑568, déc. 2019, doi: 10.3233/SJI-190564.
[4] T. Enderle, S. Giessing, et R. Tent, “Designing Confidentiality on the Fly Methodology – Three Aspects”, in Privacy in Statistical Databases, vol. 11126, J. Domingo-Ferrer et F. Montes, Éd., in Lecture Notes in Computer Science, vol. 11126. , Cham: Springer International Publishing, 2018, p. 28‑42. doi: 10.1007/978-3-319-99771-1_3.
Références (2)
Références bibliographiques
[5] T. Enderle, S. Giessing, et R. Tent, “Calculation of Risk Probabilities for the Cell Key Method”, in Privacy in Statistical Databases, vol. 12276, J. Domingo-Ferrer et K. Muralidhar, Éd., in Lecture Notes in Computer Science, vol. 12276. , Cham: Springer International Publishing, 2020, p. 151‑165. doi: 10.1007/978-3-030-57521-2_11.
[6] B. Fraser et J. Wooton, “A Proposed Method for Confidentialising Tabular Output to Protect against Differencing”, in Monographs of Official Statistics: Work Session on Statistical Data Confidentiality, 2005, p. 299‑302.
[7] S. Gießing et R. Tent, “Concepts for generalising tools implementing the cell key method to the case of continuous variables”, in UNECE - Expert Meeting on Statistical Data Confidentiality, the Hague, oct. 2019.
[8] A. Hundepool et al., Handbook on Statistical Disclosure Control, 2nd Edition, ESSNet SDC, 2024. https://sdctools.github.io/HandbookSDC/
[9] N. Shlomo, “Statistical Disclosure Control Methods for Census Frequency Tables”, Int Statistical Rev, vol. 75, nᵒ 2, p. 199‑217, août 2007, doi: 10.1111/j.1751-5823.2007.00010.x.
Merci de votre attention
Retrouvez nous sur
- Julien Jamme
- Chargé d’investissements dans les traitements de la confidentialité
- DMS/DMRG
- 0187695525
- julien.jamme@insee.fr
Séminaire interne DMS
